Pyramid Graph Neural Network: a Graph Sampling and Filtering Approach for Multi-scale Disentangled Representations

Abstract

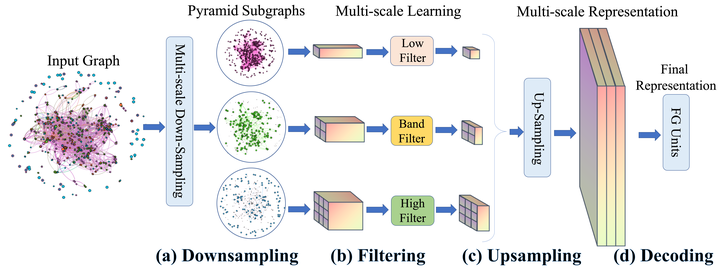
Spectral methods for graph neural networks (GNNs) have achieved great success. Despite their success, many works have shown that existing approaches are mainly focused on low-frequency information which may not be pertinent to the task at hand. Recent efforts have been made to design new graph filters for wider frequency profiles, but it remains an open problem how to learn multi-scale disentangled node embeddings in the graph Fourier domain. In this paper, we propose a graph (signal) sampling and filtering framework, entitled Pyramid Graph Neural Network (PyGNN), which follows the Downsampling-Filtering-Upsampling-Decoding scheme. To be specific, we develop the $\omega-$bandlimited downsampling approach to split input graph into subgraphs for the reduction of high-frequency components, then perform spectral graph filters on subgraphs to achieve node embeddings with different frequency bands, and propose the Laplacian smoothing-based upsampling approach to extrapolate the node embedding on subgraphs to the full set of vertices on the original graph. In the end, we add the frequency-aware gated units to decode node embeddings of different frequencies for the downstream tasks. Results on both homophilic and heterophilic graph datasets show that our proposed PyGNN model can outperform many state-of-the-art baselines for node classification.